【設題】このマッチ棒パズル、あなたならどう動かす？

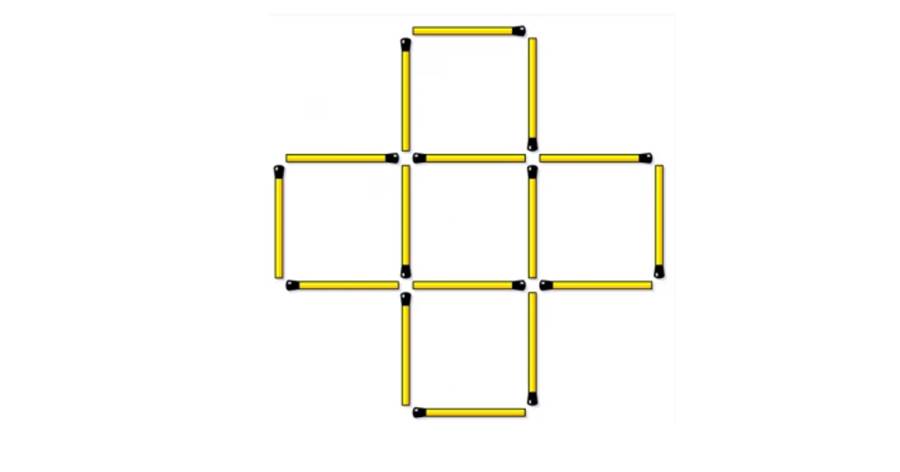
目の前にあるのは、16本のマッチ棒で作られた図形。
構造は十字型で、5つの正方形がびっしりと組まれている。

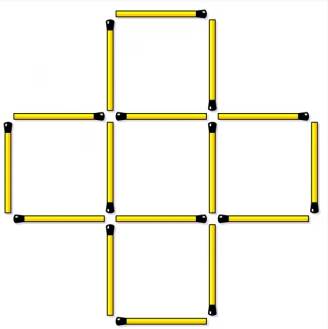
ルールはこうだ：

使用されているマッチ棒の数：16本

現在の正方形の数：5個（すべて同じ大きさ）

目的：マッチ棒を最小限だけ動かして、正方形を6個に増やすこと

制限：追加・削除は禁止。動かせるのは既存のマッチ棒のみ

さあ、あなたにこの「パズルの魔術」が見抜けるだろうか？

【観察】変えるべきは“数”ではなく“配置”

一見、完璧に並んだ5つの正方形。これ以上手を加えたらバランスが崩れそう……。
でも、よく見てみると、マッチ棒は一部の辺を共有して使われている。

つまり、1本のマッチ棒が複数の正方形に貢献しているということ。

ここが最大のポイント。
「1本の動き」が「2つ、3つの正方形」を同時に生み出す可能性があるのだ。

【思考】6つ作るには本当にマッチ棒24本が必要？

「1つの正方形＝マッチ棒4本」だから、「6つ＝24本」必要？

その理屈は普通だが、この図形は共有構造によって成り立っている。
つまり、“6つの正方形”は16本でも可能ということ。

カギは、“中央の空白”と“縦棒の再配置”。
もしその空白にマッチ棒をうまく組み込めば――？

広告

【解法】正解は「3本だけ動かす」こと！

答えは驚くほどシンプル。
中央部の空白に、横並びの正方形から3本のマッチ棒を移すだけ。

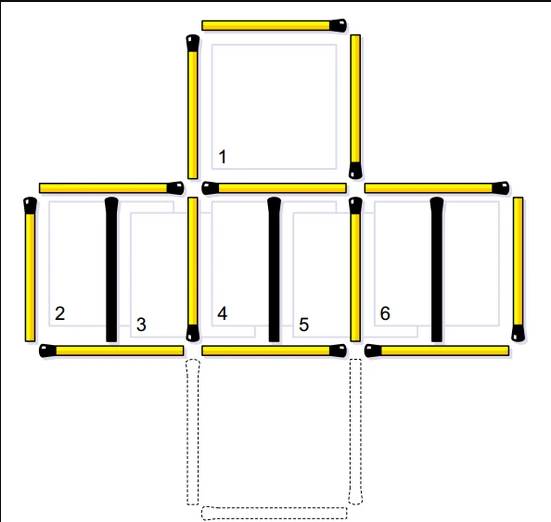
こうすることで：

もとの5つの正方形は崩れず

空白だった中央に新たな正方形が1つ追加！

これで合計6つの正方形が完成。
**「少ない動きで最大の変化を生む」**という、まさにミニマル思考の勝利！